算法之峰值查找

[front-thinking]

算法之峰值查找

峰值，英文名是Peak Finding。看过MIT算法课程的人都知道，Peak Finding被课堂上的教授称为A toy problem。这让我十分汗颜，这类问题我还是思考了很久才搞明白。峰值查找，顾名思义，就是查找数组中的峰值。数组可以分为一维数组和二维数组(更多维数组暂且不考虑)。好了，废话不多说，这里我们开始介绍峰值查找。

一维数组

这里我们先来看看一维数组的峰值查找问题，定义问题：

给出数组A，长度为n，查找数组中的一个峰值A[i]>=A[i-1]，并且A[i]>=A[i+1].

原始方法

无论多么复杂的算法问题，这里都存在原始的暴力方法来解决。这里，线性扫描数组即可，对每个元素对比是否满足条件就能解决问题。这里不再过多介绍，直接给出算法：

/*
* 1、原始暴利检索
* */
function peakFinding1DBrutSearch (arr) {
    var l = arr.length;
    if (l === 1) {
        return arr[0];
    }
    for (var i = 0; i < l; i++) {
        if (i === 0 && arr[i] > arr[i+1]) {
            return arr[i];
        }
        if (i === l - 1 && arr[i] > arr[i-1]) {
            return arr[i];
        }
        if (arr[i] > arr[i-1] && arr[i] > arr[i+1]) {
            return arr[i];
        }
    }
}

该方法的算法复杂度很容易看出来，O(n)。

二分法

虽然问题得到了解决，但是我们能否做的更好呢？这里我们想到了我们可否用二分法来降低复杂度呢。这里需要说明的一点是，我们的问题是“查找一个峰值”，而不是“判断数组是否含有峰值”，并且我们的条件是“大于等于”。这使得我们数组中肯定有峰值，否则就得另当别论了。
二分法的思路是：

1. 我们首先查找数组的中间值a[mid]；
2. 判断a[mid]是否大于a[mid+1]，大于的话对于数组前mid项继续1的步骤；
3. 否则的话，判断a[mid]是否大于a[mid-1]，大于的话对于数组mid项后面的数组继续1的步骤;
4. 不满足2和3的话，则证明元素a[mid]就是峰值，返回即可。

好了，这里需要特别注意的是边界条件，也就是数组的第一个和最后一个元素的判断。我们假定数组首尾元素只用判断它的一边就行。下面给出算法：

/*
* 2、二分法，复杂度O(logn)
* */
function peakFinding1D (arr) {
    var l = arr.length, mid = Math.floor(l/2);

    switch (true) {
        case l === 1:
            return arr[0];
            break;
        case l === 2:
            return arr[0] > arr[1] ? arr[0] : arr[1];
            break;
        default:
            break;
    }

    if (arr[mid] < arr[mid + 1]) {
        return peakFinding1D(arr.slice(mid, l));
    }
    if (arr[mid] < arr[mid - 1]) {
        return peakFinding1D(arr.slice(0, mid))
    }
    return arr[mid];
}

二维数组

二维数组，即矩阵，它的峰值不再是单个维度的判断，而是需要两个维度判断。我们先来给出定义：

给定矩阵A，n*n，查找它的一个峰值A[i, j]，使其满足A[i, j]>=A[i, j -1], A[i, j]>=A[i, j +1], A[i, j]>=A[i-1, j ], A[i, j]>=A[i+1, j].

原始方法

原始检索的方法即是检索数组中的每一个元素，判断是否满足条件。这里原始检索的方法的复杂度是O(n方)。具体算法我们不再给出，大家可以自己完成。

二分法

我们能否像一维数组一样使用二分法完成呢？答案是肯定的。聪明的你肯定想到了利用一维的情况来完成情况。例如，你可能先查找某一列或者某一行的峰值，然后判断其在行或者列上是不是也满足峰值。但是，仔细想想，这是否有问题呢。没错，就是这个问题，在某列或者某行查找的峰值，并不一定满足在对应行或者列上满足峰值。这样检查会陷入反复中。
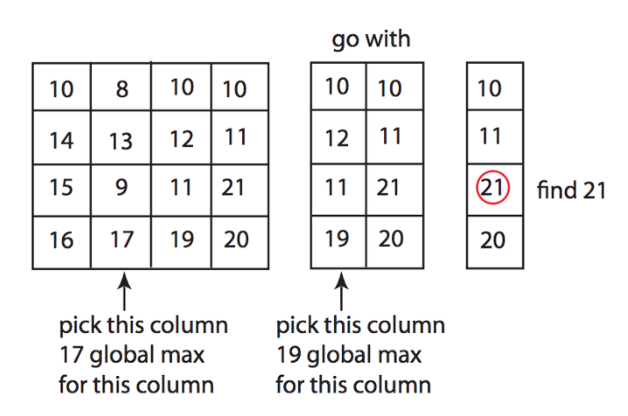
正确的方法是：

1. 查找中间列的最大值(i, j)；
2. 比较该最大值在行进行比较(i, j − 1),(i, j),(i, j + 1)；
3. 如果(i, j − 1) > (i, j)， 对前面的列进行递归1；
4. 如果(i, j) < (i, j + 1)，对后面的列进行递归1;
5. 不满足3和4，则该值就满足二维峰值，返回即可。

下面这张图是这个过程：

算法实现：

/*
* 1、二分法，复杂度O(nlogn)
* start, end是查找的起止列数
* */
function peakFinding2D (arr, start, end) {
    var l = arr.length, columns = end - start + 1, mid = Math.floor(columns/2);

    var j = findMaxIndex(arr, mid); // 先找到第mid列的最大值

    // 遍历右侧列数
    if (mid + 1 <= l && arr[j][mid] < arr[j][mid + 1]) {
        return peakFinding2D(arr, start + 1, end);
    }

    // 遍历左侧列数
    if (mid - 1 >= 0 && arr[j][mid] < arr[j][mid-1]) {
        return peakFinding2D(arr, start, end-1);
    }

    return {
        row: j,
        column: mid
    }


}

/*
* 辅助函数，查找二维数组中某一列的最大值
* */
function findMaxIndex (arr, k) {
    var l = arr.length, index = 0, max = arr[index][k];
    for (var i = 0; i < l; i++) {
        if (arr[i][k] > max) {
            max = arr[i][k];
            index = i;
        }
    }
    return index;
}

很容易得出算法复杂度为, 其中Θ(n)为与n无关的常数。则用树形画法很容易得出算法复杂度是O（nlogn）
T(n, m) = T(n, n/2) + Θ(n)