|
1 | 1 | ## 1. 图的定义 |
2 | 2 |
|
3 | | -> **图(Graph)**:由顶点集合 $V$ 与边集合 $E$(顶点之间的关系)构成的数据结构。图的形式化定义为 $G = (V, E)$。 |
| 3 | +> **图(Graph)**:由顶点集合 $V$ 和边集合 $E$(即顶点之间的连接关系)组成的数据结构,通常记作 $G = (V, E)$。 |
4 | 4 |
|
5 | | -- **顶点(Vertex)**:图中的基本元素,通常称为顶点,表示对象或节点。顶点的集合 $V$ 是有限非空集合,包含 $n > 0$ 个顶点。如下面的示意图所示,通常我们使用圆圈来表示顶点。 |
6 | | -- **边(Edge)**:顶点之间的关系或连接。边的形式化定义为:$e = \langle u, v \rangle$,表示从 $u$ 到 $v$ 的一条边,其中 $u$ 称为起始点,$v$ 称为终止点。如下面的示意图所示,通常我们使用连接两个顶点的线段来表示边。 |
| 5 | +- **顶点(Vertex)**:图的基本单元,表示对象或节点。顶点集合 $V$ 是有限且非空的,包含 $n > 0$ 个顶点。通常用圆圈表示顶点。 |
| 6 | +- **边(Edge)**:连接两个顶点的线段,表示它们之间的关系。边可记为 $e = \langle u, v \rangle$,表示从 $u$ 到 $v$ 的一条边,其中 $u$ 是起点,$v$ 是终点。 |
7 | 7 |
|
8 | 8 |  |
9 | 9 |
|
10 | | -- **子图(Sub Graph)**:对于图 $G = (V, E)$ 与 $G^{'} = (V^{'}, E^{'})$,如果满足 $V^{'} \subseteq V$,$E^{'} \subseteq E$,则称图 $G^{'}$ 是图 $G$ 的一个子图。直观的说,子图是由原图的一部分顶点和边组成的,同时边的两端顶点必须属于子图的顶点集合 $V^{'}$。特别地,根据定义,图 $G$ 本身也是其一个子图。在下图中,我们展示了一个图 $G$ 及其子图 $G^{'}$。 |
| 10 | +- **子图(Sub Graph)**:如果图 $G' = (V', E')$ 满足 $V' \subseteq V$ 且 $E' \subseteq E$,则 $G'$ 是 $G$ 的子图。也就是说,子图由原图部分顶点和边组成,且边的两个端点都属于 $V'$。特别地,$G$ 本身也是它的一个子图。下图展示了图 $G$ 及其子图 $G'$。 |
11 | 11 |
|
12 | 12 | 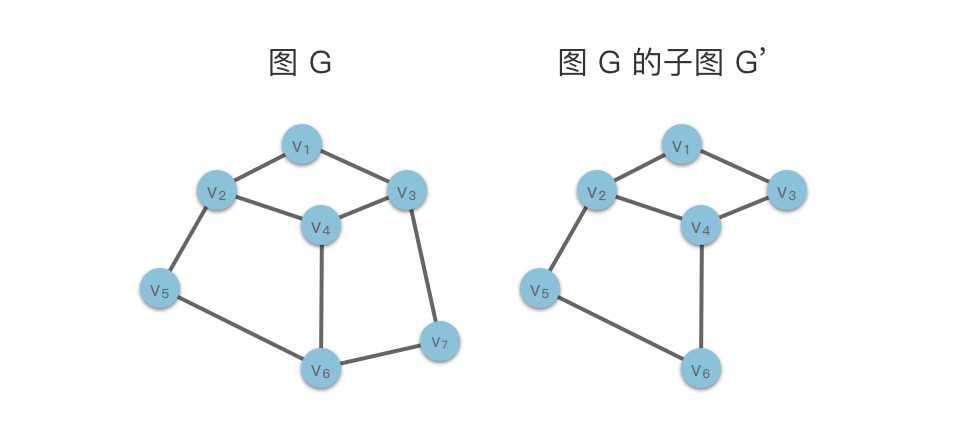 |
13 | 13 |
|
14 | 14 | ## 2. 图的分类 |
15 | 15 |
|
16 | | -### 2.1 无向图和有向图 |
| 16 | +### 2.1 无向图与有向图 |
17 | 17 |
|
18 | | -根据边是否具有方向性,图可以分为两种类型:「无向图」和「有向图」。 |
| 18 | +按边是否有方向,可以将图分为「无向图」和「有向图」。 |
19 | 19 |
|
20 | | -> **无向图(Undirected Graph)**:如果图中每条边都没有方向性,则称为无向图。例如,表示朋友关系或者城市间双向行驶的路线图常用无向图建模。 |
| 20 | +- **无向图(Undirected Graph)**:边没有方向,常用于表示朋友关系、城市间双向道路等。无向图的边由两个顶点组成的无序对表示,如下图左侧中的顶点 $(v_1, v_2)$。 |
21 | 21 |
|
22 | | -在无向图中,每条边都是由两个顶点组成的无序对。例如下图左侧中的顶点 $v_1$ 和顶点 $v_2$ 之间的边记为 $(v_1, v_2)$ 或 $(v_2, v_1)$。 |
23 | | - |
24 | | -> **有向图(Directed Graph)**:如果图中的每条边都具有方向性,则称为有向图。例如,表示任务流程的流程图或网络请求的依赖图是典型的有向图。 |
25 | | -
|
26 | | -在有向图中,有向边(又称弧)是由两个顶点组成的有序对,例如下图右侧中从顶点 $v_1$ 到顶点 $v_2$ 的弧,记为 $\langle v_1, v_2 \rangle$,$v_1$ 被称为弧尾,$v_2$ 被称为弧头,如下图所示。 |
| 22 | +- **有向图(Directed Graph)**:边有方向,常用于表示任务流程、依赖关系等。有向图的边(弧)由两个顶点组成的有序对表示,如下图右侧中的顶点 $\langle v_1, v_2 \rangle$,其中 $v_1$ 为弧尾,$v_2$ 为弧头。 |
27 | 23 |
|
28 | 24 | 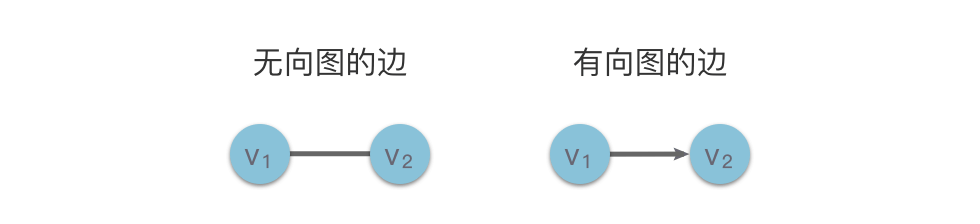 |
29 | 25 |
|
30 | | -如果图中有 $n$ 个顶点,则根据图的类型,其边(或弧)的最大数量可以定义如下: |
| 26 | +如果图有 $n$ 个顶点,则: |
31 | 27 |
|
32 | | -- **无向图中边的最大数量**:在无向图中,任意两个顶点之间最多存在一条边,因此最多可以有 $\frac{n \times (n - 1)}{2}$ 条边。具有 $\frac{n \times (n - 1)}{2}$ 条边的无向图称为 **「完全无向图(Completed Undirected Graph)」**。 |
| 28 | +- **无向图最大边数**:$\frac{n \times (n - 1)}{2}$。达到最大边数的无向图称为 **完全无向图**。 |
| 29 | +- **有向图最大边数**:$n \times (n - 1)$。达到最大边数的有向图称为 **完全有向图**。 |
33 | 30 |
|
34 | | -- **有向图中边的最大数量**:在有向图中,任意两个顶点之间可以存在一对方向相反的弧,因此最多可以有 $n \times (n - 1)$ 条弧。具有 $n \times (n - 1)$ 条弧的有向图称为 **「完全有向图(Completed Directed Graph)」**。 |
35 | | - |
36 | | -下图展示了两个示例:左侧为包含 $4$ 个顶点的完全无向图,右侧为包含 $4$ 个顶点的完全有向图。 |
| 31 | +下图左为 $4$ 个顶点的完全无向图,右为 $4$ 个顶点的完全有向图: |
37 | 32 |
|
38 | 33 | 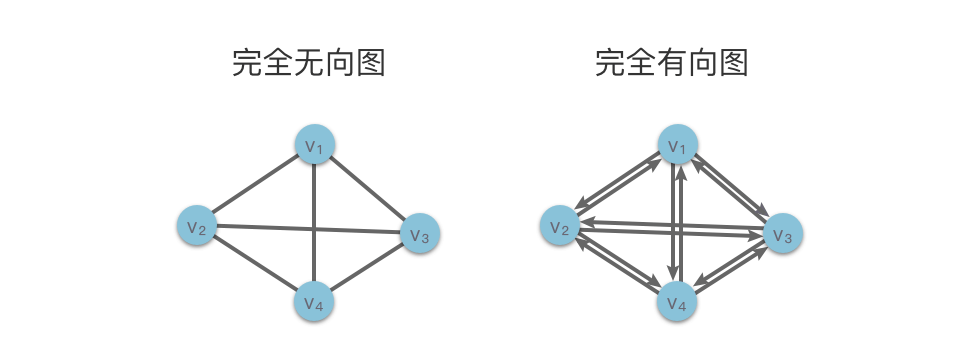 |
39 | 34 |
|
40 | | -下面介绍一下无向图和有向图中一个重要概念 **「顶点的度」**。 |
41 | | - |
42 | | -> **顶点的度**:与该顶点 $v_i$ 相关联的边的数量,记为 $TD(v_i)$。 |
| 35 | +**顶点的度** 是图的一个重要概念: |
43 | 36 |
|
44 | | -- **无向图中顶点的度**:在无向图中,顶点的都是与该顶点相连的边的数量。例如,在上图左侧的完全无向图中,顶点 $v_3$ 的度为 $3$,因为有 $3$ 个其他的顶点与 $v_3$ 相连接。 |
45 | | - |
46 | | -- **有向图中顶点的度**:在有向图中,顶点的度可以分为「出度」和「入度」两个部分。 |
47 | | - - **出度(Out Degree)**:以该顶点 $v_i$ 为出发点的边的条数,记为 $OD(v_i)$。 |
48 | | - - **入度(In Degree)**:以该顶点 $v_i$ 为终止点的边的条数,记为 $ID(v_i)$。 |
49 | | - |
50 | | -在有向图中,顶点 $v_i$ 的度是该点出度和入度之和,即:$TD(v_i) = OD(v_i) + ID(v_i)$。 |
51 | | - |
52 | | -例如,在上图右侧的完全有向图中,顶点 $v_3$ 的出度为 $3$,入度为 $3$,因此顶点 $v_3$ 的度为 $3 + 3 = 6$。 |
| 37 | +- **无向图中,顶点的度**:与该顶点相连的边的数量,记为 $TD(v_i)$。 |
| 38 | + - 如上图左,$v_3$ 的度为 $3$。 |
| 39 | +- **有向图中,顶点的度** 分为: |
| 40 | + - **出度(Out Degree)**:以该顶点为起点的边数,记为 $OD(v_i)$。 |
| 41 | + - **入度(In Degree)**:以该顶点为终点的边数,记为 $ID(v_i)$。 |
| 42 | + - 顶点总度:$TD(v_i) = OD(v_i) + ID(v_i)$。 |
| 43 | + - 如上图右,$v_3$ 的出度为 $3$,入度为 $3$,总度为 $6$。 |
53 | 44 |
|
54 | 45 | ### 2.2 环形图和无环图 |
55 | 46 |
|
56 | | -> **路径** :图中的一个重要概念,对于图 $G = (V, E)$,如果存在顶点序列 $v_{i_0}, v_{i_1}, v_{i_2}, …, v_{i_m}$,并且每对相邻的顶点都有图中的边连接,即 $(v_{i_0}, v_{i_1}), (v_{i_1}, v_{i_2}), …, (v_{i_{m-1}}, v_{i_m}) \in E$(对于有向图则是 $\langle v_{i_0}, v_{i_1} \rangle, \langle v_{i_1}, v_{i_2} \rangle, …, \langle v_{i_{m-1}}, v_{i_m} \rangle \in E$),则称该顶点序列为从顶点 $v_{i_0}$ 和顶点 $v_{i_m}$ 之间的一条路径,其中 $v_{i_0}$ 是这条路径的起始点,$v_{i_m}$ 是这条路径的终止点。 |
57 | | -
|
58 | | -简而言之,如果顶点 $v_{i_0}$ 可以通过一系列的顶点和边到达顶点 $v_{i_m}$,则称这两个顶点之间有一条路径,其中经过的顶点序列则称为两个顶点之间的路径。 |
| 47 | +> **路径**:路径是图论中的核心概念。对于图 $G = (V, E)$,如果存在顶点序列 $v_{i_0}, v_{i_1}, v_{i_2}, \ldots, v_{i_m}$,使得任意相邻顶点对之间都存在边相连(无向图为 $(v_{i_{k-1}}, v_{i_k}) \in E$,有向图为 $\langle v_{i_{k-1}}, v_{i_k} \rangle \in E$,$1 \leq k \leq m$),则称该顶点序列为从 $v_{i_0}$ 到 $v_{i_m}$ 的一条路径。其中,$v_{i_0}$ 为起点,$v_{i_m}$ 为终点。 |
59 | 48 |
|
60 | | -- **环(Circle)**:如果一条路径的起始点和终止点相同(即 $v_{i_0} == v_{i_m}$ ),则称这条路径为「回路」或「环」。 |
| 49 | +简而言之,如果从顶点 $v_{i_0}$ 出发,经过若干顶点和边能够到达顶点 $v_{i_m}$,则称 $v_{i_0}$ 与 $v_{i_m}$ 之间存在一条路径,所经过的顶点序列即为这条路径。 |
61 | 50 |
|
62 | | -- **简单路径**:顶点序列中顶点不重复出现的路径称为「简单路径」。 |
| 51 | +- **环(Cycle)**:如果一条路径的起点和终点重合(即 $v_{i_0} = v_{i_m}$),则称该路径为「环」或「回路」。 |
| 52 | +- **简单路径**:路径上所有顶点均不重复出现(除非是环的首尾重合),称为「简单路径」。 |
63 | 53 |
|
64 | | -根据图中是否有环,我们可以将图分为「环形图」和「无环图」。 |
| 54 | +根据图中是否存在环,可以将图分为「环形图」和「无环图」: |
65 | 55 |
|
66 | | -- **环形图(Circular Graph)**:如果图中存在至少一条环路,则该图称为「环形图」。 |
67 | | -- **无环图(Acyclic Graph)**:如果图中不存在环路,则该图称为「无环图」。 |
| 56 | +- **环形图(Circular Graph)**:如果图中至少存在一条环,则称为环形图。 |
| 57 | +- **无环图(Acyclic Graph)**:如果图中不存在任何环,则称为无环图。 |
68 | 58 |
|
69 | | -在有向图中,如果不存在环路,则将该图称为「有向无环图(Directed Acyclic Graph, DAG)」。有向无环图因其独特的拓扑结构,广泛应用于诸如动态规划、最短路径问题、数据压缩等算法场景。 |
| 59 | +对于有向图,如果不存在环,则称为「有向无环图(Directed Acyclic Graph, DAG)」。DAG 结构在动态规划、最短路径、数据压缩等算法中有着广泛应用。 |
70 | 60 |
|
71 | | -下图展示了四种图的类型:无向无环图、无向环形图、有向无环图和有向环形图。在有向环形图中,顶点 $v_1$、$v_2$、$v_3$ 与相连的边构成了一个环。 |
| 61 | +下图展示了四类典型图结构:无向无环图、无向环形图、有向无环图和有向环形图。其中有向环形图中,顶点 $v_1$、$v_2$、$v_3$ 及其相连的边构成了一个环。 |
72 | 62 |
|
73 | 63 | 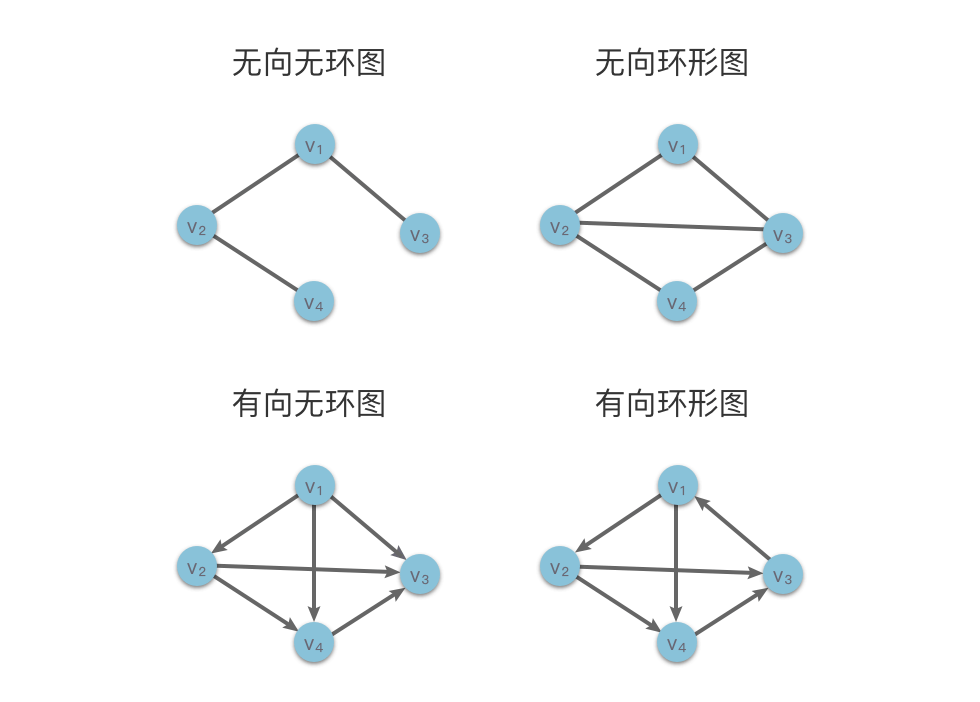 |
74 | 64 |
|
75 | | -### 2.3 连通图和非连通图 |
| 65 | +### 2.3 连通图与非连通图 |
76 | 66 |
|
77 | 67 | #### 2.3.1 连通无向图 |
78 | 68 |
|
79 | | -在无向图中,如果存在一条从顶点 $v_i$ 到顶点 $v_j$ 的路径,则称顶点 $v_i$ 和 $v_j$ 是连通的。 |
| 69 | +在无向图中,如果从顶点 $v_i$ 能通过一条路径到达顶点 $v_j$,则称 $v_i$ 和 $v_j$ 连通。 |
80 | 70 |
|
81 | | -- **连通无向图**:如果无向图中任意两个顶点之间都是连通的(即任意两个顶点之间都有路径连接),则称该图为「连通无向图」。 |
82 | | -- **非连通无向图**:如果无向图中存在至少一对顶点之间没有任何路径连接,则称该图为「非连通无向图」。 |
| 71 | +- **连通无向图**:任意两个顶点之间都有路径相连的无向图。 |
| 72 | +- **非连通无向图**:存在至少一对顶点之间没有路径相连的无向图。 |
83 | 73 |
|
84 | | -下图展示了两种情况: |
85 | | - |
86 | | -- 在左侧图中,顶点 $v_1$ 与所有其他顶点 $v_2$、$v_3$、$v_4$、$v_5$、$v_6$ 都是连通的,因此该图为连通无向图。 |
87 | | -- 在右侧图中,顶点 $v_1$ 与 $v_2$、$v_3$、$v_4$ 是连通的,但与 $v_5$、$v_6$ 没有任何路径连接,因此该图为非连通无向图。 |
| 74 | +下图左侧为连通无向图,$v_1$ 能与所有其他顶点连通;右侧为非连通无向图,$v_1$ 只能与 $v_2$、$v_3$、$v_4$ 连通,无法到达 $v_5$、$v_6$。 |
88 | 75 |
|
89 | 76 | 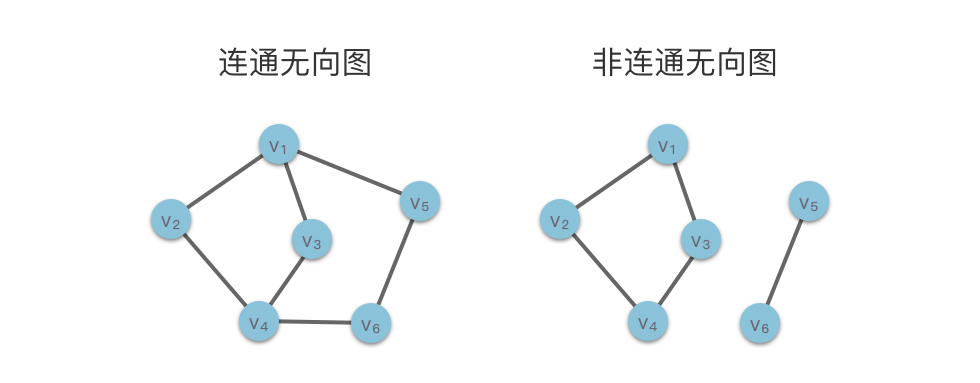 |
90 | 77 |
|
91 | 78 | #### 2.3.2 无向图的连通分量 |
92 | 79 |
|
93 | | -在无向图中,某些图可能不是连通的,但它们的子图可能是连通的。这样的子图称为「连通子图」。对于其中某个连通子图,如果不存在任何包含他的更大连通子图,则该连通子图称为「连通分量」。 |
| 80 | +在无向图中,整体可能不是连通的,但其中的某些子图是连通的,这些子图称为「连通子图」。如果一个连通子图无法再被包含于更大的连通子图中,则称其为「连通分量」,即无向图中的极大连通子图。 |
94 | 81 |
|
95 | | -- **连通子图**:如果无向图的子图是连通的,则该子图称为连通子图。 |
96 | | -- **连通分量**:无向图中的一个极大连通子图(不存在任何包含它的更大的连通子图)称为该图的连通分量。 |
97 | | -- **极⼤连通⼦图**:无向图中的一个连通子图,且不存在包含它的更大的连通子图。 |
| 82 | +- **连通子图**:无向图的一个子图,且该子图是连通的。 |
| 83 | +- **极大连通子图**:连通子图中,如果不存在包含它的更大的连通子图,则称为极大连通子图。 |
| 84 | +- **连通分量**:无向图中的极大连通子图,即为该图的连通分量。 |
98 | 85 |
|
99 | | -例如,上图右侧的非连通无向图中,尽管整体图是非连通的,但顶点 $v_1$、$v_2$、$v_3$、$v_4$ 与其相连的边构成的子图是连通的,并且不存在任何包含它的更大的连通子图,因此该子图是原图的一个连通分量。类似地,顶点 $v_5$、$v_6$ 与其相连的边也构成了原图的另一个连通分量。 |
| 86 | +举例来说,上图右侧的非连通无向图中,顶点 $v_1$、$v_2$、$v_3$、$v_4$ 及其相连的边构成了一个连通子图,且无法再扩展为更大的连通子图,因此它是原图的一个连通分量。同理,顶点 $v_5$、$v_6$ 及其相连的边也构成了另一个连通分量。 |
100 | 87 |
|
101 | 88 | #### 2.3.3 强连通有向图 |
102 | 89 |
|
103 | | -在有向图中,如果从顶点 $v_i$ 到 $v_j$ 存在路径,且从顶点 $v_j$ 到 $v_i$ 也有路径,则称顶点 $v_i$ 与 $v_j$ 是「强连通」的。 |
104 | | - |
105 | | -- **强连通有向图**:如果图中任意两个顶点 $v_i$ 和 $v_j$ 都满足从 $v_i$ 到 $v_j$ 和从 $v_j$ 到 $v_i$ 均有路径,则称该图为「强连通有向图」。 |
106 | | -- **非强连通有向图**:如果图中存在至少一对顶点之间没有路径连接(即无法相互到达),则称该图为「非强连通有向图」。 |
| 90 | +在有向图中,如果顶点 $v_i$ 能到达 $v_j$,且 $v_j$ 也能到达 $v_i$,则称 $v_i$ 和 $v_j$ 是「强连通」的。 |
107 | 91 |
|
108 | | -下图展示了两种情况: |
| 92 | +- **强连通有向图**:任意两个顶点都能互相到达的有向图。 |
| 93 | +- **非强连通有向图**:存在至少一对顶点不能互相到达的有向图。 |
109 | 94 |
|
110 | | -- 左侧图中,任意两个顶点之间都存在路径,因此该图为强连通有向图。 |
111 | | -- 右侧图中,顶点 $v_7$ 无法通过路径到达其他顶点,因此该图为非强连通有向图。 |
| 95 | +下图左为强连通有向图,任意两点可互达;右图中 $v_7$ 无法到达其他顶点,因此不是强连通有向图。 |
112 | 96 |
|
113 | 97 |  |
114 | 98 |
|
115 | 99 | #### 2.3.4 有向图的强连通分量 |
116 | 100 |
|
117 | | -在有向图中,「强联通分量」是指其内部任意两个顶点之间都强连通的极大强连通子图。以下是具体定义: |
| 101 | +在有向图中,「强连通分量」指的是:图中某个极大子图,子图内任意两个顶点都可以互相到达(即强连通),并且无法再加入其他顶点使其仍然强连通。 |
118 | 102 |
|
119 | | -- **强连通子图**:有向图的一个子图,且该子图中任意两个顶点都是强连通的。 |
120 | | -- **极⼤强连通⼦图**:如果一个强联通子图不能被包含在任何更大的强连通子图中,则称其为极大强连通子图。 |
121 | | -- **强连通分量**:有向图中的一个极⼤强连通⼦图,称为该图的强连通分量。 |
| 103 | +简要定义如下: |
122 | 104 |
|
123 | | -举个例子来解释一下。 |
| 105 | +- **强连通子图**:有向图的一个子图,子图内任意两点互相可达。 |
| 106 | +- **极大强连通子图**:不能再加入其他顶点的强连通子图。 |
| 107 | +- **强连通分量**:有向图中的极大强连通子图。 |
124 | 108 |
|
125 | | -例如,上图右侧的非强连通有向图,其本身不是强连通的(因为顶点 $v_7$ 无法通过路径到达其他顶点)。但顶点 $v_1$、$v_2$、$v_3$、$v_4$、$v_5$、$v_6$ 与它们之间的边构成了一个强连通子图(即上图的左侧图),且不存在包含它的更大的强连通子图,因此这是右侧图的一个强连通分量。类似地,顶点 $v_7$ 构成了一个只有一个顶点的强连通子图,因此它自身也是右侧图的一个强连通分量。 |
| 109 | +举例说明:上图右侧的有向图不是强连通图(如 $v_7$ 无法到达其他顶点),但 $v_1$、$v_2$、 |
| 110 | +$v_3$、$v_4$、$v_5$、$v_6$ 及其边构成了一个强连通分量(即左侧图)。而 $v_7$ 自身也单独构成一个强连通分量。 |
126 | 111 |
|
127 | 112 | ### 2.4 带权图 |
128 | 113 |
|
129 | | -有时,图不仅需要表示顶点之间是否存在某种关系,还需要表示这一关系的具体细节。有时候我们需要给边赋予一些数据信息,这些数据信息被称为 **权**。在具体应用中,权值可以具有某种具体意义,比如权值可以代表距离、时间以及价格等不同属性。 |
| 114 | +有些图不仅表示顶点之间是否有关系,还需要描述这种关系的「强度」或「代价」,这就是「权」。权值可以表示距离、时间、费用等。 |
130 | 115 |
|
131 | | -- **带权图**:如果图的每条边都被赋以⼀个权值,则该图称为带权图。权值通常表示一个非负实数,但在某些场景下也可以是负数。 |
132 | | -- **网络**:带权的连通⽆向图被称为⽹络。 |
| 116 | +- **带权图**:每条边都带有权值的图。权值一般为非负数,有时也可以为负数。 |
| 117 | +- **网络**:带权且连通的无向图称为网络。 |
133 | 118 |
|
134 | | -在下面的示意图中,我们给出了一个带权图的例子。 |
| 119 | +下图展示了一个带权图的例子: |
135 | 120 |
|
136 | 121 | 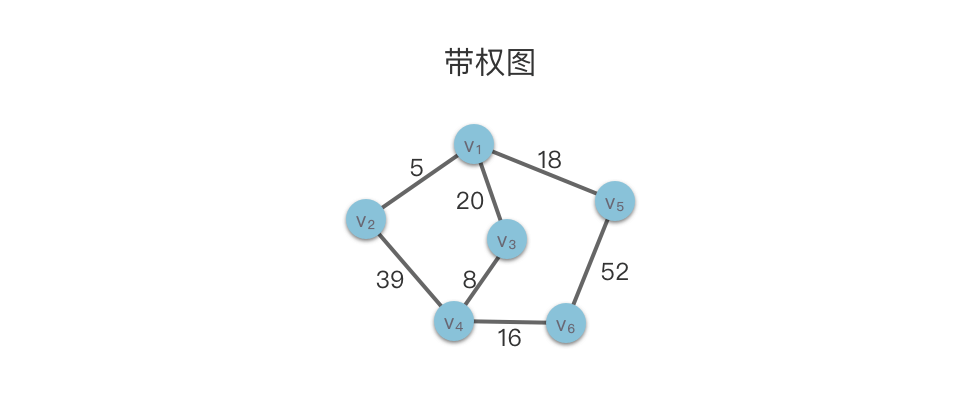 |
137 | 122 |
|
138 | | -### 2.5 稠密图和稀疏图 |
| 123 | +### 2.5 稠密图与稀疏图 |
| 124 | + |
| 125 | +图按边的多少可分为「稠密图」和「稀疏图」,这一划分没有严格的界限,仅为便于理解。 |
| 126 | + |
| 127 | +- **稠密图(Dense Graph)**:边数接近完全图的图,即大多数顶点之间都有边相连。 |
| 128 | +- **稀疏图(Sparse Graph)**:边数远少于完全图的图(常见如 $e < n \times \log_2 n$),大部分顶点之间没有直接连接。 |
| 129 | + |
| 130 | +## 3. 总结 |
| 131 | + |
| 132 | +图是计算机科学中最重要的数据结构之一,由顶点和边组成,用于表示对象间的关系。本文介绍了图的基本概念和分类: |
| 133 | + |
| 134 | +### 核心概念 |
| 135 | +- **顶点(Vertex)**:图的基本单元,表示对象或节点 |
| 136 | +- **边(Edge)**:连接顶点的线段,表示对象间的关系 |
| 137 | +- **路径**:顶点序列,表示从一个顶点到另一个顶点的遍历过程 |
| 138 | + |
| 139 | +### 主要分类 |
| 140 | +1. **按方向性**:无向图(双向关系)vs 有向图(单向关系) |
| 141 | +2. **按连通性**:连通图(任意两点可达)vs 非连通图(存在孤立部分) |
| 142 | +3. **按环结构**:环形图(存在回路)vs 无环图(无回路,如DAG) |
| 143 | +4. **按权值**:带权图(边有权重)vs 无权图(边无权重) |
| 144 | +5. **按密度**:稠密图(边多)vs 稀疏图(边少) |
139 | 145 |
|
140 | | -根据图中边的稀疏程度,我们可以将图分为「稠密图」和「稀疏图」。这是一个模糊的概念,目前为止还没有给出一个量化的定义。 |
| 146 | +### 重要特性 |
| 147 | +- **度**:无向图中顶点的连接数,有向图中分为入度和出度 |
| 148 | +- **连通分量**:无向图中的极大连通子图 |
| 149 | +- **强连通分量**:有向图中任意两点互相可达的极大子图 |
141 | 150 |
|
142 | | -- **稠密图(Dense Graph)**:有很多条边或弧(边的条数 $e$ 接近于完全图的边数)的图称为稠密图。 |
143 | | -- **稀疏图(Sparse Graph)**:有很少条边或弧(边的条数 $e$ 远小于完全图的边数,如 $e < n \times \log_2n$)的图称为稀疏图。 |
| 151 | +理解这些基础概念是学习图算法(如 DFS、BFS、最短路径、最小生成树等)的重要前提。 |
144 | 152 |
|
145 | 153 | ## 参考资料 |
146 | 154 |
|
|
0 commit comments