Skip to content

Commit f2cee4e

Browse files
itchargeitcharge
committed
修复和优化语句表述
1 parent 73ce833 commit f2cee4e

File tree

1 file changed

+113
-50
lines changed

1 file changed

+113
-50
lines changed

‎docs/04_string/04_07_string_sunday.md‎

Lines changed: 113 additions & 50 deletions
Original file line numberDiff line numberDiff line change
@@ -1,100 +1,163 @@
11
## 1. Sunday 算法介绍
22

3-
**「Sunday 算法」** 是一种在字符串中查找子串的算法，是 Daniel M.Sunday 于1990年提出的字符串模式匹配算法。
3+
> **Sunday 算法**：Sunday 算法是一种高效的字符串查找算法，由 Daniel M. Sunday 于 1990 年提出，专门用于在主串中查找子串的位置。
4+
>
5+
> - **核心思想**：对于给定的文本串 $T$ 和模式串 $p$，Sunday 算法首先对模式串 $p$ 进行预处理，生成一个「后移位数表」。在匹配过程中，每当发现不匹配时，算法会根据文本串中参与本轮匹配的末尾字符的「下一个字符」，决定模式串应向右滑动的距离，从而尽可能跳过无效的比较，加快匹配速度。
46
5-
> **Sunday 算法思想**：对于给定文本串 $T$ 与模式串 $p$，先对模式串 $p$ 进行预处理。然后在匹配的过程中，当发现文本串 $T$ 的某个字符与模式串 $p$ 不匹配的时候，根据启发策略，能够尽可能的跳过一些无法匹配的情况，将模式串多向后滑动几位。
7+
Sunday 算法的思想与 Boyer-Moore 算法类似，但 Sunday 算法始终从左到右进行匹配。当匹配失败时，Sunday 算法关注的是文本串 $T$ 当前匹配窗口末尾的下一个字符 $T[i + m]$，并据此决定模式串的滑动距离，实现快速跳跃。
68

7-
Sunday 算法思想跟 Boyer Moore 算法思想类似。不同的是，Sunday 算法匹配顺序是从左向右，并且在模式串 $p$ 匹配失败时关注的是文本串 $T$ 中参加匹配的末尾字符的下一位字符。当文本串 $T$ 中某个字符跟模式串 $p$ 的某个字符不匹配时，可以将模式串 $p$ 快速向右移动。
9+
具体来说，遇到不匹配时有两种情况：
810

9-
遇到不匹配字符时，可以根据以下两种情况向右快速进行移动：
10-
11-
- **情况 1：文本串 $T$ 中与模式串 $p$ 尾部字符 $p[m - 1]$ 对应的字符下一个位置的字符 $T[i + m]$ 出现在模式串 $p$ 中**。
12-
- 这种情况下，可将$T[i + m]$ 与模式串中最后一次出现的该字符对齐，如下图所示。
13-
- **向右移动位数 = 文本串 $T$ 中与模式串 $p$ 尾部位置的下一个位置 $T[i + m]$ 在模式串中最后一次出现的位置**。
14-
- 注意：文本串 $T$ 中与模式串 $p$ 尾部位置的下一个位置其实就是「模式串长度」。
11+
- **情况 1：$T[i + m]$ 出现在模式串 $p$ 中**
12+
- 此时，将模式串 $p$ 向右移动，使其最后一次出现 $T[i + m]$ 的位置与 $T[i + m]$ 对齐。
13+
- **向右移动的位数 = 模式串中 $T[i + m]$ 最右侧出现的位置到末尾的距离**
14+
- 说明：$T[i + m]$ 即为当前匹配窗口末尾的下一个字符。
1515

1616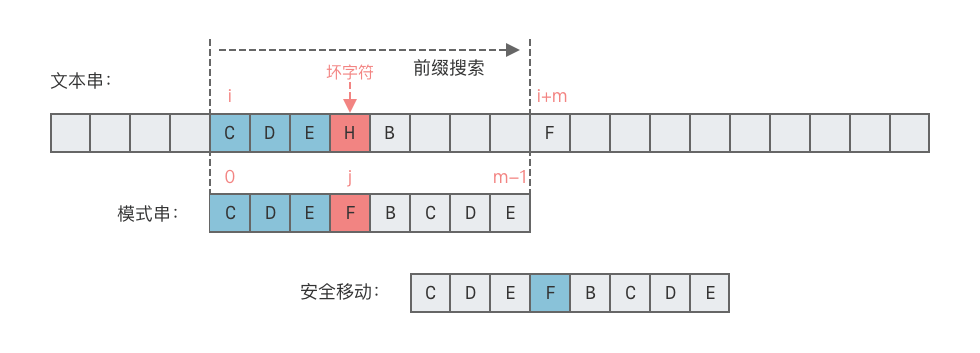
![Sunday 算法情况 1](https://qcdn.itcharge.cn/images/20240511165526.png)
1717

18-
- **情况 2：文本串 $T$ 中与模式串 $p$ 尾部字符 $p[m - 1]$ 对应的字符下一个位置的字符 $T[i + m]$ 没有出现在模式串 $p$ 中**。
19-
- 这种情况下，可将模式串整个右移，如下图所示。
20-
- **向右移动位数 = 整个模式串长度 + 1**。
18+
- **情况 2：$T[i + m]$ 未出现在模式串 $p$ 中**
19+
- 此时，直接将模式串整体向右移动 $m + 1$ 位。
20+
- **向右移动的位数 = 模式串长度 $m + 1$**
2121

2222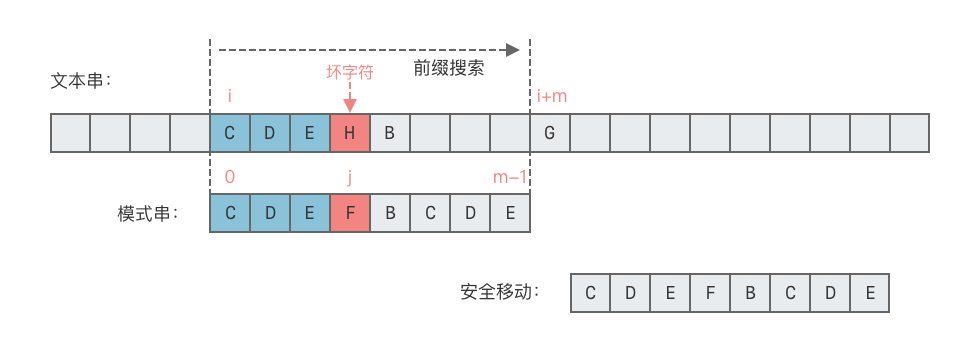
![Sunday 算法情况 2](https://qcdn.itcharge.cn/images/20240511165540.png)
2323

2424
## 2. Sunday 算法步骤
2525

26-
整个 Horspool 算法步骤描述如下：
26+
Sunday 算法的具体流程如下：
2727

28-
- 计算出文本串 $T$ 的长度为 $n$，模式串 $p$ 的长度为 $m$。
29-
- 先对模式串 $p$ 进行预处理，生成后移位数表 $bc\underline{\hspace{0.5em}}table$。
30-
- 将模式串 $p$ 的头部与文本串 $T$ 对齐，将 $i$ 指向文本串开始位置，即 $i = 0$。$j$ 指向模式串开始，即 $j = 0$，然后从模式串开始位置开始比较。
31-
- 如果文本串对应位置的字符 $T[i + j]$ 与模式串对应字符 $p[j]$ 相同，则继续比较后一位字符。
32-
- 如果模式串全部匹配完毕，则返回模式串 $p$ 在文本串中的开始位置 $i$。
33-
- 如果文本串对应位置的字符 $T[i + j]$ 与模式串对应字符 $p[j]$ 不同，则：
34-
- 根据后移位数表 $bc\underline{\hspace{0.5em}}table$ 和模式串末尾位置对应的文本串上的字符 $T[i + m]$ ，计算出可移动距离 $bc\underline{\hspace{0.5em}}table[T[i + m]]$，然后将模式串进行后移。
35-
- 如果移动到末尾也没有找到匹配情况，则返回 $-1$。
28+
- 设文本串 $T$ 长度为 $n$，模式串 $p$ 长度为 $m$。
29+
- 首先对模式串 $p$ 进行预处理，生成后移位数表 $bc\underline{\hspace{0.5em}}table$。
30+
- 令 $i = 0$，表示当前模式串 $p$ 的起始位置与文本串 $T$ 的第 $i$ 位对齐。
31+
- 在每一轮匹配中，从头开始比较 $T[i + j]$ 与 $p[j]$（$j$ 从 $0$ 到 $m-1$）：
32+
- 如果所有字符均匹配，则返回当前匹配的起始位置 $i$。
33+
- 如果出现不匹配，或未全部匹配完毕，则：
34+
- 检查 $T[i + m]$（即当前匹配窗口末尾的下一个字符）：
35+
- 如果 $T[i + m]$ 存在于后移位数表中，则将 $i$ 增加 $bc\underline{\hspace{0.5em}}table[T[i + m]]$，即将模式串向右滑动相应距离。
36+
- 如果 $T[i + m]$ 不存在于后移位数表中，则将 $i$ 增加 $m + 1$，即整体右移 $m + 1$ 位。
37+
- 若遍历完整个文本串仍未找到匹配，则返回 $-1$。
3638

3739
## 3. Sunday 算法代码实现
3840

3941
### 3.1 后移位数表代码实现
4042

41-
生成后移位数表的代码实现比较简单，跟 Horspool 算法中生成后移位数表的代码差不多。具体步骤如下：
43+
后移位数表的实现非常简洁，与 Horspool 算法类似。具体思路如下：
4244

43-
- 使用一个哈希表 $bc\underline{\hspace{0.5em}}table$， $bc\underline{\hspace{0.5em}}table[bad\underline{\hspace{0.5em}}char]$ 表示表示遇到坏字符可以向右移动的距离。
44-
- 遍历模式串，以当前字符 $p[i]$ 为键，可以向右移动的距离（$m - i$）为值存入字典中。如果出现重复字符，则新的位置下标值会将之前存放的值覆盖掉。这样哈希表中存放的就是该字符在模式串中出现最右侧位置上的可向右移动的距离。
45+
- 使用一个哈希表 $bc\underline{\hspace{0.5em}}table$，其中 $bc\underline{\hspace{0.5em}}table[bad\underline{\hspace{0.5em}}char]$ 表示遇到该字符时，模式串可以向右移动的距离。
46+
- 遍历模式串 $p$，将每个字符 $p[i]$ 作为键，其对应的移动距离 $m - i$ 作为值存入字典。如果字符重复出现，则以最右侧（下标最大的）位置为准，覆盖之前的值。这样，哈希表中存储的就是每个字符在模式串中最右侧出现时可向右移动的距离。
4547

46-
如果在 Sunday 算法的匹配过程中，如果 $T[i + m]$ 不在 $bc\underline{\hspace{0.5em}}table$ 中时，可令其为 $m + 1$，表示可以将模式串整个右移到上一次匹配末尾后边两个位置上。如果 $T[i + m]$ 在 $bc\underline{\hspace{0.5em}}table$ 中时，可移动距离就是 $bc\underline{\hspace{0.5em}}table[T[i + m]]$ 。这样就能计算出可以向右移动的位数了。
48+
在 Sunday 算法匹配过程中，如果 $T[i + m]$ 不在 $bc\underline{\hspace{0.5em}}table$ 中，则默认移动 $m + 1$ 位，即将模式串整体右移到当前匹配窗口末尾的下一个字符之后。如果 $T[i + m]$ 存在于表中，则移动距离为 $bc\underline{\hspace{0.5em}}table[T[i + m]]$。这样即可高效计算每次滑动的步长。
4749

48-
生成后移位数表的代码如下：
50+
后移位数表的代码如下：
4951

5052
```python
51-
# 生成后移位数表
52-
# bc_table[bad_char] 表示遇到坏字符可以向右移动的距离
53+
# 生成 Sunday 算法的后移位数表
54+
# bc_table[bad_char] 表示遇到坏字符 bad_char 时，模式串可以向右移动的距离
5355
def generateBadCharTable(p: str):
56+
"""
57+
构建 Sunday 算法的后移位数表。
58+
输入:
59+
p: 模式串
60+
输出:
61+
bc_table: 字典，key 为字符，value 为遇到该字符时可向右移动的距离
62+
"""
5463
m = len(p)
5564
bc_table = dict()
56-
57-
for i in range(m): # 迭代到最后一个位置 m - 1
58-
bc_table[p[i]] = m - i # 更新遇到坏字符可向右移动的距离
65+
# 遍历模式串的每一个字符（包括最后一个字符）
66+
for i in range(m):
67+
# 对于每个字符 p[i]，记录其对应的移动距离
68+
# 移动距离 = 模式串长度 - 当前字符下标
69+
bc_table[p[i]] = m - i
70+
# 如果字符重复出现，保留最右侧（下标最大）的距离
5971
return bc_table
6072
```
6173

6274
### 3.2 Sunday 算法整体代码实现
6375

6476
```python
65-
# sunday 算法，T 为文本串，p 为模式串
77+
# Sunday 算法实现，T 为文本串，p 为模式串
6678
def sunday(T: str, p: str) -> int:
79+
"""
80+
Sunday 算法主函数，返回模式串 p 在文本串 T 中首次出现的位置，若未匹配则返回 -1。
81+
参数:
82+
T: 文本串
83+
p: 模式串
84+
返回:
85+
int: 第一个匹配位置的下标，未匹配返回 -1
86+
"""
6787
n, m = len(T), len(p)
68-
69-
bc_table = generateBadCharTable(p) # 生成后移位数表
70-
71-
i = 0
88+
if m == 0:
89+
return 0 # 空模式串视为匹配在开头
90+
91+
bc_table = generateBadCharTable(p) # 生成后移位数表
92+
93+
i = 0 # i 表示当前窗口在文本串中的起始下标
7294
while i <= n - m:
95+
# 逐字符比较当前窗口是否与模式串完全匹配
7396
j = 0
74-
if T[i: i + m] == p:
75-
return i # 匹配完成，返回模式串 p 在文本串 T 的位置
97+
while j < m and T[i + j] == p[j]:
98+
j += 1
99+
if j == m:
100+
return i # 匹配成功，返回起始下标
101+
# 检查窗口末尾的下一个字符，决定滑动距离
76102
if i + m >= n:
77-
return -1
78-
i += bc_table.get(T[i + m], m + 1) # 通过后移位数表，向右进行进行快速移动
79-
return -1 # 匹配失败
80-
81-
# 生成后移位数表
82-
# bc_table[bad_char] 表示遇到坏字符可以向右移动的距离
103+
return -1 # 已到文本串末尾，未匹配
104+
next_char = T[i + m] # 当前窗口末尾的下一个字符
105+
# 若 next_char 在后移位数表中，滑动对应距离，否则滑动 m+1
106+
shift = bc_table.get(next_char, m + 1)
107+
i += shift
108+
return -1 # 未找到匹配
109+
110+
# 生成 Sunday 算法的后移位数表
111+
# bc_table[bad_char] 表示遇到坏字符 bad_char 时，模式串可以向右移动的距离
83112
def generateBadCharTable(p: str):
113+
"""
114+
构建 Sunday 算法的后移位数表。
115+
参数:
116+
p: 模式串
117+
返回:
118+
dict: 字典，key 为字符，value 为遇到该字符时可向右移动的距离
119+
"""
84120
m = len(p)
85121
bc_table = dict()
86-
87-
for i in range(m): # 迭代到最后一个位置 m - 1
88-
bc_table[p[i]] = m - i # 更新遇到坏字符可向右移动的距离
122+
# 遍历模式串每个字符（包括最后一个字符）
123+
for i in range(m):
124+
# 记录每个字符在模式串中最右侧出现时可向右移动的距离
125+
bc_table[p[i]] = m - i
89126
return bc_table
90127

91-
print(sunday("abbcfdddbddcaddebc", "aaaaa"))
92-
print(sunday("abbcfdddbddcaddebc", "bcf"))
128+
# 测试用例
129+
print(sunday("abbcfdddbddcaddebc", "aaaaa")) # 输出: -1，未匹配
130+
print(sunday("abbcfdddbddcaddebc", "bcf")) # 输出: 2，匹配成功
93131
```
94132

95133
## 4. Sunday 算法分析
96134

97-
- Sunday 算法在平均情况下的时间复杂度为 $O(n)$，但是在最坏情况下时间复杂度会退化为 $O(n * m)$。
135+
| 指标 | 复杂度 | 说明 |
136+
| ------------ | ---------------- | ------------------------------------------------------------ |
137+
| 最好时间复杂度 | $O(n)$ | 模式串字符分布均匀，后移位数表能实现最大跳跃，比较次数最少。 |
138+
| 最坏时间复杂度 | $O(n \times m)$ | 模式串字符高度重复且与文本不匹配时，每次只能滑动一位。 |
139+
| 平均时间复杂度 | $O(n)$ | 实际应用中通常接近最好情况，比较次数较少。 |
140+
| 空间复杂度 | $O(m + \sigma)$ | 主要用于存储后移位数表，$m$ 为模式串长度，$\sigma$ 为字符集大小。 |
141+
142+
- $n$ 为文本串长度，$m$ 为模式串长度，$\sigma$ 为字符集大小。
143+
- Sunday 算法在大多数实际场景下效率较高，但极端情况下可能退化为 $O(n \times m)$。
144+
- 空间消耗主要体现在后移位数表的构建上。
145+
146+
## 5. 总结
147+
148+
Sunday 算法是一种高效的字符串匹配算法，通过利用窗口末尾字符的后移位数表，实现大步跳跃式匹配，提升了实际查找效率，适用于大多数文本搜索场景。
149+
150+
**优点**：
151+
- 实现简单，易于理解和编码。
152+
- 平均性能优良，实际应用中匹配效率高。
153+
- 只需构建一次后移位数表，预处理开销小。
154+
- 跳跃能力强，适合大多数实际文本搜索场景。
155+
156+
**缺点**：
157+
- 最坏情况下时间复杂度较高，可能退化为 $O(n \times m)$。
158+
- 只利用窗口末尾字符的信息，未充分利用更多启发式规则（如 BM 算法的好后缀规则）。
159+
- 对极端重复或特殊构造的模式串不够友好，跳跃能力有限。
160+
98161

99162
## 参考资料
100163

0 commit comments

Comments
 (0)